基于双卡尔曼算法的锂离子电池SOC和SOH的联合在线估计，采用带遗忘因子递推最小二乘法（FFRLS）进行参数辨识（含MATLAB代码）

于 2024-06-10 19:15:01 发布
阅读量2.4k 收藏 33
点赞数 23
CC 4.0 BY-SA版权
文章标签： matlab 最小二乘法 算法
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接： https://blog.csdn.net/weixin_54001429/article/details/139578763

一、电池等效电路模型的选择

等效电路模型考虑到计算精度和时间复杂度，选取二阶RC等效电路模型。电路图如下所示：

二、模型的参数辨识

模型的参数辨识方法采用在线参数辨识的带遗忘因子递推最小二乘法（FFRLS），该算法是从最小二乘法经过优化得到的，优化流程如下所示：

具体应用流程略（可参考其他资料，有详细的推导过程），电池不同工况的放电数据可通过开源数据集获取也可通过实验获取（最终整理需要得到4个参数：电池端电压，电池电流，电池参考的RSOC值，数据采样时间）。 注意遗忘因子ff取值需要非常靠近1（例如0.99999），取得小可能导致估计产生较大的误差，也可以通过不断的调整改善参数估计的效果。 以下是FFRLS方法实现参数辨识方法的MATLAB代码（此处包装成函数形式，方便之后的算法调用），可直接通过代码来单独验证参数辨识的精确度（需要注意的是此时必须保证精确度较高后续的电池状态估计才会比较准确，即 端电压误差最好在电池最大电压的1%以下，误差小的话估计效果才好，此时后续的SOC估计才有意义 ），同时也可通过搭建Simulink模型来通过输入参数得到模拟端电压，思路同理。 

% 传入参数在调用函数的代码中会有解释
function [R0, R1, R2, C1, C2, error_U, V1] = FFRLS(Vot, Cur, RSOC, Ts, p, ff, c0)

%% 变量初始化（可根据实际情况进行调整）
p0 = 10^(-1) * eye(5, 5);

T = length(Vot);
R0 = zeros(1, T); R1 = zeros(1, T); R2 = zeros(1, T); C1 = zeros(1, T); C2 = zeros(1, T);
c = zeros(5, T);
error = zeros(1, T);
error_U = zeros(1, T);
V1 = zeros(1, T);
c(:, 1) = c0;
c(:, 2) = c(:, 1);
U1 = 0; U2 = 0;

%% 带遗忘因子递推最小二乘法
for k = 3:T
    Uoc1 = OCV_SOC_Func(k - 1, p, RSOC); Uoc2 = OCV_SOC_Func(k - 2, p, RSOC); Uoc = OCV_SOC_Func(k, p, RSOC);
   
    h = [(Uoc1 - Vot(k - 1)), (Uoc2 - Vot(k - 2)), Cur(k), Cur(k - 1), Cur(k - 2)]';
    x = h' * p0 * h + ff;
    
    Kk = p0 * h / x;
    error(k) = (Uoc - Vot(k)) - h' * c(:, k - 1);
    c(:, k) = c(:, k - 1) + Kk * error(k);
    p1 = (p0 - Kk * h' * p0) / ff;
    p0 = p1;
%% 参数计算和分离
    k1 = c(1, k); k2 = c(2, k); k3 = c(3, k); k4 = c(4, k); k5 = c(5, k);
    k0 = Ts^2 / (1 - k1 - k2);
    a = -k0 * k2;
    b = k0 * (k1 + 2 * k2) / Ts;
    C = k0 * (k3 + k4 + k5) / Ts^2;
    d = -k0 * (k4 + 2 * k5) / Ts;

    dd = (b^2 - 4 * a);
    t1 = abs((b + sqrt(dd))) / 2;
    t2 = abs((b - sqrt(dd))) / 2;
    
    R0(k) = abs(k5 / k2);
    R1(k) = ((t1 * C + t2 * R0(k) - d) / (t1 - t2));
    R2(k) = (C - R0(k) - R1(k));
    C1(k) = (t1 / R1(k));
    C2(k) = (t2 / R2(k));
    
%% 辨识结果精确度分析验证（通过参数模拟端电压与真实端电压得到误差，模拟端电压通过全响应方程得到）
    e1 = (U1 - Cur(k - 1) * R1(k - 1)) * exp(-Ts / t1);
    e2 = (U2 - Cur(k - 1) * R2(k - 1)) * exp(-Ts / t2);
    U1 = Cur(k) * R1(k) + e1;
    U2 = Cur(k) * R2(k) + e2;
    V1(k) = Uoc - Cur(k) * R0(k) - U1 - U2;
    error_U(k) = V1(k) - Vot(k);
end
% 以下是给参数值设置前两个数组位置的初值，防止调用时数组前两个位置没有值而报错
R0(1) = R0(3); R0(2) = R0(3);
R1(1) = R1(3); R1(2) = R1(3);
R2(1) = R2(3); R2(2) = R2(3);
C1(1) = C1(3); C1(2) = C1(3);
C2(1) = C2(3); C2(2) = C2(3);
end

三、锂离子电池SOC与SOH联合估计

首先要介绍的是卡尔曼算法，卡尔曼算法的流程可如下图所示：

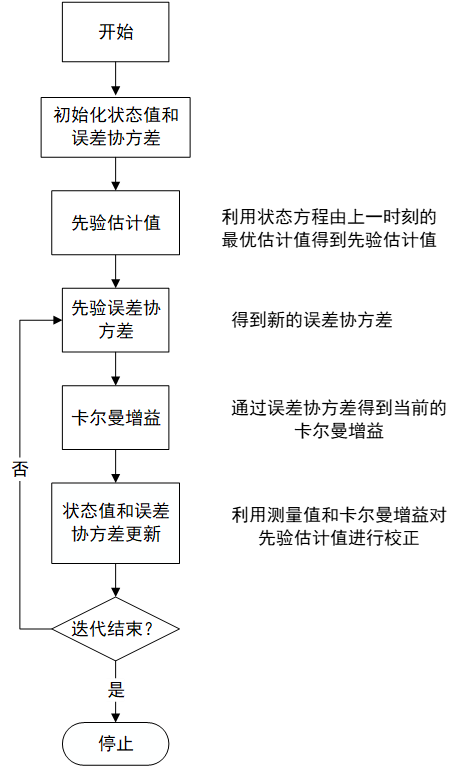
卡尔曼算法的具体证明过程和公式推导可参考其他资料（推荐B站的up主DR_CAN的关于卡尔曼算法的证明和分析），本篇文章不再赘述。由于 考虑到电池内部化学反应的非线性，使用扩展卡尔曼算法对电池系统进行线性化 ，之后采用朴素卡尔曼算法的计算流程完成电池SOC的估计。

通过卡尔曼算法的步骤和原理不难看出，要使用卡尔曼算法的关键点有以下几个：

  1. 状态量和测量值的选择以及测量值的真实值和估计值。
  2. 状态方程和测量方程的选择与列写。
  3. 初值的设置。

本文选取的时较为常见的状态量为 X_k=[U_1,U_2,SOC_K] ，测量值为端电压 U_{ekf} ，端电压真实值在电池数据中可以获取到，可以通过电路方程离散化后得到相应的状态和测量方程，进而运用卡尔曼算法对电池SOC进行估计。初值的选取一般需要根据不同的数据进行调整，取值一般为较小的数（例如1e-3,1e-4），需要根据实时估计的效果进行修改。

进行电池SOH估计时，则选取状态量 X_k=C_{ekf} ，即状态量为容量本身（本文通过容量估算来推算到电池的SOH值），测量方程选择对电池SOC定义的方程，具体如下式所示： d_k=SOC_k-SOC_{k-1}+\frac{I_{k-1}T_s}{C_{max,k-1}}+\varepsilon ，我自己的解释是电池SOC值的变化是由于有电流而引起的，所以SOC的变化值可以用电流来表示， d_k 的真实值应该为0。原理差不多就这么多，接下来看看代码（这里使用了联合估计，在一个循环中引入两个卡尔曼滤波器分别对SOC和SOH进行估计，而两个估计的值可以用在另一个滤波器的方程计算中）： 

%% 模型参数
E0 = 1e-6; E1 = 1e-3; ff = 0.99999;
load('HPPC.mat'); % 放电数据
discharge = HPPC(:, :); % 2584
load('OCV_SOC_70Ah.mat');% OCV-SOC关系
Qn = 70 * 3600; % 容量，单位：A * s
Ts = 0.1; % 采样间隔

%% 初始值
Q = E0 * eye(3); % 估计误差协方差
R = 0.1; N = E0; % 测量误差协方差
Px0 = [E1 0 0;0 E1 0;0 0 1]; % 状态误差协方差初始值
Pc0 = [E1];
M = E0; % 容量变化矩阵

%% 赋值
tm = discharge(1, :); % 时间
Cur = discharge(2, :); % 电流
Vot = discharge(3, :); % 测量得到的端电压
RSOC = discharge(4, :) / Qn * 3600; % SOC真实值-安时法计算得到
T = length(tm); % 时间
c0 = [Vot(1), Vot(2), Cur(3), Cur(2), Cur(1)];

%% OCV-SOC关系曲线拟合多项式
x = OCV_SOC_70Ah(2, :); % SOC
y = OCV_SOC_70Ah(1, :); % OCV
p = polyfit(x, y, 8); % 多项式参数值

%% EKF算法估计SOC和SOH
% 初始化参数 状态量Xekf、开路电压Uoc、端电压Vekf、卡尔曼增益K、观测矩阵H
Xekf = [0; 0; 0.4]; % [U1, U2, SOC]初始值
C_ekf = zeros(1, T); % 电池容量初始值
C_ekf(1) = Qn;
[R0, R1, R2, C1, C2, error_U, V1] = FFRLS(Vot, Cur, RSOC, Ts, p, ff, c0); % 初始化模型参数
% [R0, R1, R2, C1, C2, error_U, V1] = KF_Parameter(Vot, Cur, RSOC, Ts, p);

Uoc = zeros(1, T); % 初始化OCV
Vekf = zeros(1, T); % 初始化端电压值
d = zeros(1 ,T); % 初始化SOH估算的测量值
Kc = zeros(1, T); % 电阻估算的卡尔曼增益
SOH = zeros(1, T);
Kx = zeros(3, T); % 卡尔曼增益
Hx = zeros(T, 3); Hc = zeros(T, 1); % 观测矩阵

SOH(1) = 1; % SOH估计值
Uoc(1) = p(1) * Xekf(3)^8 + p(2) * Xekf(3)^7 + p(3) * Xekf(3)^6 + p(4) * Xekf(3)^5 + p(5) * Xekf(3)^4 + p(6) * Xekf(3)^3 + p(7) * Xekf(3)^2 + p(8) * Xekf(3) + p(9); % 初始化OCV
C = [-1 -1 0];
Vekf(1) = Uoc(1) + C * Xekf - Cur(1) * R0(1); % 估计出端电压的值（Ud = Uocv - U1 - U2 - IR）

for i = 1:T - 1
    % 系统矩阵更新
    A = [1 - Ts/R1(i)/C1(i) 0 0; 0 1 - Ts/R2(i)/C2(i) 0; 0 0 1]; % 系统矩阵
    B = [Ts/C1(i); Ts/C2(i); -Ts/C_ekf(i)];

    Xekf(:, i + 1) = A * Xekf(:, i) + B * Cur(i + 1); % 先验状态值（状态估计方程）
    C_ekf(i + 1) = C_ekf(i);
    
    % 通过估计的SOC在OCV-SOC曲线得到估计的开路电压值
    Uoc(i+1) = polyval(p, Xekf(3, i + 1));
    
    Hx(i,:)=[-1 -1 p(1)*8*Xekf(3,i+1)^7+p(2)*7*Xekf(3,i+1)^6+p(3)*6*Xekf(3,i+1)^5+p(4)*5*Xekf(3,i+1)^4+p(5)*4*Xekf(3,i+1)^3+p(6)*3*Xekf(3,i+1)^2+p(7)*2*Xekf(3,i+1)+p(8)]; % 观测矩阵更新
    Hc(i) = -Cur(i + 1) * Ts / C_ekf(i + 1)^2;
    
    Vekf(i + 1) = Uoc(i + 1) + C * Xekf(:, i + 1) - Cur(i + 1) * R0(i); % 估计得到的端电压值（测量方程）
    d(i + 1) = Xekf(3, i + 1) - Xekf(3, i) + Cur(i) * Ts / C_ekf(i);
    
    Px = A * Px0 * A' + Q; % 计算先验状态误差协方差
    Pc = Pc0 + M;
    
    Kx(:, i) = Px * Hx(i, :)' / (Hx(i, :) * Px * Hx(i, :)' + R); % 更新卡尔曼增益
    Kc(i) = Pc * Hc(i) / (Hc(i) * Pc * Hc(i) + N);
    
    Xekf(:, i + 1) = Xekf(:, i + 1) + Kx(:, i) * (Vot(i + 1) - Vekf(i + 1)); % 得到后验最优估计状态值，并更新到下一个时刻的初始值
    C_ekf(i + 1) = C_ekf(i + 1) + Kc(i) * (-d(i + 1));
    
    Px0 = (eye(3) - Kx(:, i) * Hx(i, : )) * Px; % 更新状态误差协方差
    Pc0 = (1 - Kc(i) * -Cur(i) * Ts / C_ekf(i)^2) * Pc;
    
    SOH(i + 1) = C_ekf(i + 1) / Qn;
end

代码中其实并没有真正实现在线估计，因为是将参数存在了一个数组中，再通过不断取值进行SOC和SOH的估计，这是因为我不喜欢频繁调用函数，浪费太多资源，例如有的数据可能高达上百万组就需要调函数上百万次。读者可以自行通过代码运行加以体会。但当数据需要动态获取时，就不可避免的要频繁调用函数了。相应的值都已在代码中求出，画图需要自己另外根据自己的需求编写代码。还需要注意的是OCV-SOC曲线的获取，这条曲线我们获取的目的是通过开路电压的值我们可以得到电池SOC的值，而曲线是通过是使用少数几个数据点进行曲线拟合成高阶函数曲线来得到（ 通过HPPC阶段性放电曲线，可取SOC的值为0.1、0.2、0.3...1这些特殊点的值比较准确 ）。在调用代码时需要注意数据的顺序要和代码一一对应，且工况数据根据需求修改即可。最终 SOC估算的误差在最好在1%到3%之内 ，误差太大可依次检查参数辨识的精确度，参数初值的设置以及迭代方程的正确性。电池SOH的估算最好是获取到电池全寿命周期的数据，这样SOH的值变化会更加明显，估算的效果会更好。

大体内容就这么多，细节部分需要自己去理解，查找更多资料，代码也需要多调试，算法流程也可以多去理解推导。希望大家能通过这篇文章有所收获！